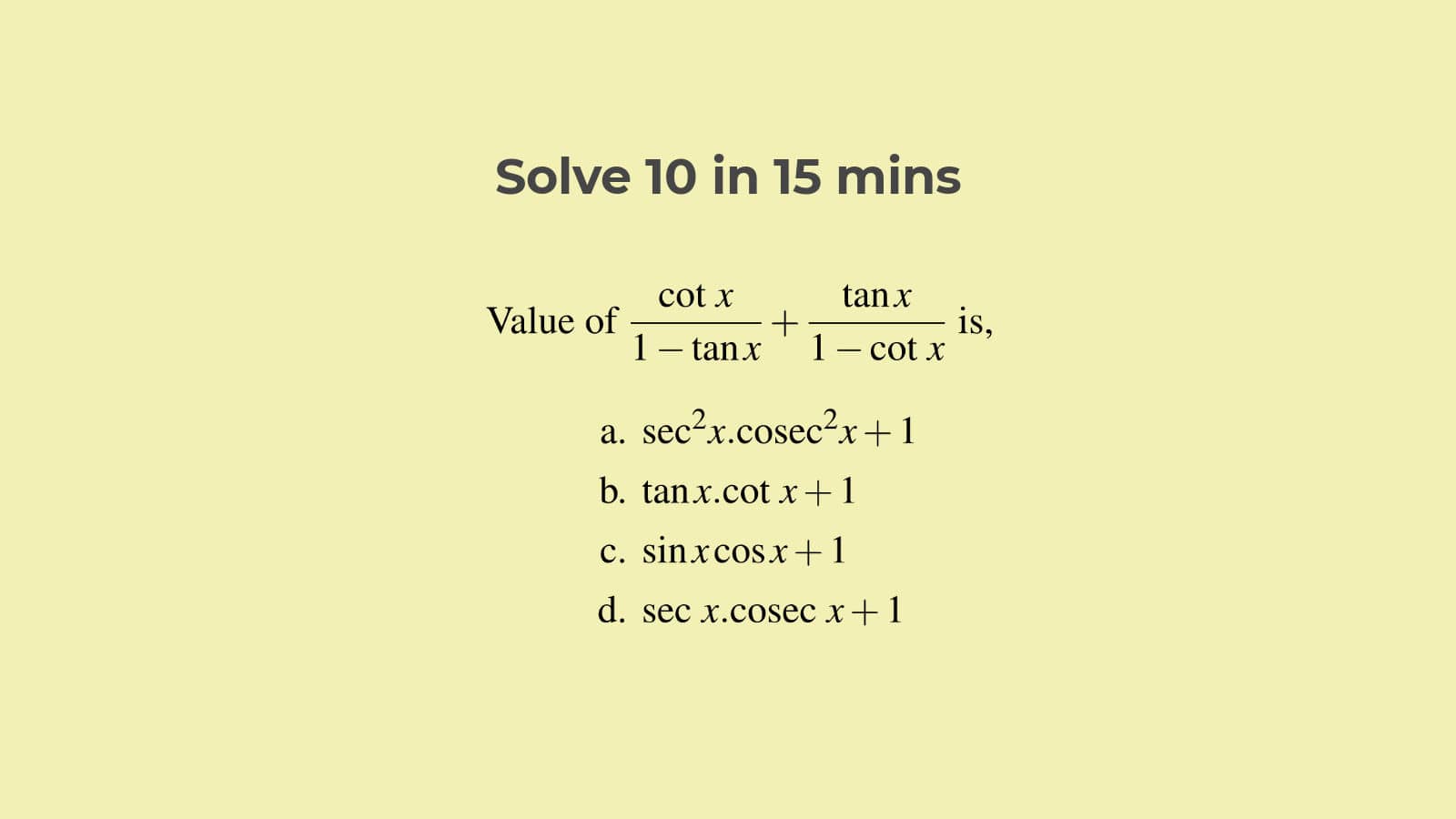
2nd Set of 10 Trigonometry questions for SSC CPO with answers and quick solutions
Trigonometry problem solving questions for SSC CPO Set 2. Verify from answers and learn how to solve quick from solutions. Previous year questions.
The solved question set contains,
- Question set on Trigonometry for SSC CPO to be answered in 15 minutes (10 chosen questions)
- Answers to the questions, and
- Quick conceptual solutions to the questions.
Take the timed test, verify correctness from answers and learn to solve quick from solutions.
Trigonometry questions for SSC CPO Set 2 - answering time 15 mins
Q1. What is the value of $\sin 8\theta+\sin 6\theta$?
- $2\sin 7\theta\cos \theta$
- $2\sin 4\theta\cos 3\theta$
- $2\sin 7\theta\cos 7\theta$
- $2\sin \theta\cos 7\theta$
Q2. If $5\sin x=4$, then numerical value of $\left(\displaystyle\frac{\tan x-\text{cot }x}{\text{sec }x-\tan x}\right)\left(\displaystyle\frac{\cos^4 x-\sin^4 x}{2\cos^2 x-1}\right)$ is,
- $\displaystyle\frac{9}{5}$
- $\displaystyle\frac{7}{4}$
- $\displaystyle\frac{3}{5}$
- $\displaystyle\frac{5}{4}$
Q3. What is the value of $\displaystyle\frac{\sin \theta}{1-\text{cot }\theta}-\displaystyle\frac{\cos \theta}{1-\tan \theta}$?
- $\displaystyle\frac{1}{(\sin \theta-\cos \theta)}$
- $\displaystyle\frac{1}{(\sin \theta+\cos \theta)}$
- $\sin \theta+\cos \theta$
- $\sin \theta-\cos \theta$
Q4. The value of $\sin^2 30^0.\cos^2 45^0+2\tan^2 30^0-\text{sec}^2 60^0$ is equal to,
- $-\displaystyle\frac{13}{12}$
- $-\displaystyle\frac{1}{12}$
- $-\displaystyle\frac{77}{24}$
- $-\displaystyle\frac{25}{12}$
Q5. If $\tan x=\text{cot }(45^0+2x)$, then what is the value of $x$?
- $20^0$
- $45^0$
- $\displaystyle\frac{45^0}{2}$
- $15^0$
Q6. If $\sin (A+B)=\displaystyle\frac{\sqrt{3}}{2}$ and $\tan (A-B)=\displaystyle\frac{1}{\sqrt{3}}$, then $(2A+3B)$ is equal to,
- $125^0$
- $135^0$
- $120^0$
- $130^0$
Q7. What is the value of $\displaystyle\frac{\text{cot }x}{1-\tan x}+\displaystyle\frac{\tan x}{1-\text{cot }x}$?
- $\text{sec}^2 x.\text{cosec}^2 x+1$
- $\tan x.\text{cot }x+1$
- $\sin x\cos x+1$
- $\text{sec } x.\text{cosec } x+1$
Q8. What is the least value of $15\cos^2 \theta+17\sin^2 \theta$?
- $2$
- $18$
- $15$
- $14$
Q9. If $\cos 37^0=\displaystyle\frac{a}{b}$ then what is the value of $\text{cosec }37^0-\cos 53^0$?
- $\displaystyle\frac{b\sqrt{a^2+b^2}}{a}$
- $\displaystyle\frac{b^2-a^2}{ab}$
- $\displaystyle\frac{a^2}{b\sqrt{a^2+b^2}}$
- $\displaystyle\frac{a^2}{b\sqrt{b^2-a^2}}$
Q10. If $\displaystyle\frac{\text{cot}^2 x}{(1+\sqrt{3})}+\displaystyle\frac{1}{2}(3-\sqrt{3})=\text{cot }x$, what is the value of $x$?
- $\displaystyle\frac{\pi}{2}$, $\displaystyle\frac{\pi}{4}$
- $\pi$, $\displaystyle\frac{\pi}{4}$
- $\displaystyle\frac{\pi}{6}$, $\displaystyle\frac{\pi}{4}$
- $\displaystyle\frac{\pi}{6}$, $\displaystyle\frac{\pi}{2}$
Answers to the Trigonometry questions for SSC CPO Set 2
Q1. Answer: Option a: $2\sin 7\theta\cos \theta$.
Q2. Answer: Option b: $\displaystyle\frac{7}{4}$.
Q3. Answer: Option a: $\displaystyle\frac{1}{\sin \theta-\cos \theta}$.
Q4. Answer: Option c: $-\displaystyle\frac{77}{24}$.
Q5. Answer: Option d: $15^0$.
Q6. Answer: Option b: $135^0$.
Q7. Answer: Option d: $\text{sec } x.\text{cosec } x+1$
Q8. Answer: Option c: $15$.
Q9. Answer: Option d: $\displaystyle\frac{a^2}{b\sqrt{b^2-a^2}}$.
Q10. Answer: Option c: $\displaystyle\frac{\pi}{6}$, $\displaystyle\frac{\pi}{4}$.
Solutions to the Trigonometry questions for SSC CPO Set 2 - answering time 15 mins
Q1. What is the value of $\sin 8\theta+\sin 6\theta$?
- $2\sin 7\theta\cos \theta$
- $2\sin 4\theta\cos 3\theta$
- $2\sin 7\theta\cos 7\theta$
- $2\sin \theta\cos 7\theta$
Solution 1: Immediate solution by Key pattern identification of two angle values $A=7\theta$ and $B=\theta$ to give $(A+B)=8\theta$, and $(A-B)=6\theta$ as in the given expression
The key point is to identify first from the choice values and the given expression that compound angle expansions in the form of $\sin (A+B)$ are required for both the terms in the given expression.
And then, the critical identification of two angle values, $A=7\theta$ and $B=\theta$ that will give us,
$8\theta=7\theta+\theta=A+B$ and $6\theta=7\theta-\theta=A-B$.
The given expression,
$\sin 8\theta+\sin 6\theta=\sin (7\theta+\theta)+\sin (7\theta-\theta)$
$=(\sin 7\theta\cos \theta+\cos 7\theta\sin \theta)+(\sin 7\theta\cos \theta-\cos 7\theta\sin \theta)$
$=2\sin 7\theta\cos \theta$.
Answer: Option a: $2\sin 7\theta\cos \theta$.
Key concepts used: Compound angle trigonometric functions -- Key pattern identification -- Solving in mind.
Q2. If $5\sin x=4$, then numerical value of $\left(\displaystyle\frac{\tan x-\text{cot }x}{\text{sec }x-\tan x}\right)\left(\displaystyle\frac{\cos^4 x-\sin^4 x}{2\cos^2 x-1}\right)$ is,
- $\displaystyle\frac{9}{5}$
- $\displaystyle\frac{7}{4}$
- $\displaystyle\frac{3}{5}$
- $\displaystyle\frac{5}{4}$
Solution 2: Quick solution by key pattern identification of second factor becoming 1 and then substituting simple values of the trigonometric functions obtained from value of $\sin x$
The key pattern identified is that the second factor simplifies to just 1.
The numerator of the second factor is simplified to,
$\cos^4 x-\sin^4 x$
$=(\cos^2 x-\sin^2 x)(\cos^2 x+\sin^2 x)=(\cos^2 x-\sin^2 x)$.
The denominator is also transformed to the same form,
$2\cos^2 x-1=(\cos^2 x-\sin^2 x)$.
With second factor simplified to 1, the target expression becomes,
$E=\left(\displaystyle\frac{\tan x-\text{cot }x}{\text{sec }x-\tan x}\right)$.
From given equation, value of $\sin x=\displaystyle\frac{4}{5}$.
So,
$\cos x=\sqrt{1-\sin^2 x}=\displaystyle\frac{3}{5}$,
$\tan x=\displaystyle\frac{4}{3}$,
$\text{cot }x=\displaystyle\frac{3}{4}$,
$\tan x-\text{cot }=\displaystyle\frac{7}{12}$,
$\text{sec }x=\displaystyle\frac{5}{3}$,
$\text{sec }x-\tan x=\displaystyle\frac{1}{3}$.
In this case, it is easier to evaluate the individual values of the functions and then the numerator and denominator. The value of the target expression is,
$E=\left(\displaystyle\frac{\tan x-\text{cot }x}{\text{sec }x-\tan x}\right)$
$=\displaystyle\frac{\displaystyle\frac{7}{12}}{\displaystyle\frac{1}{3}}=\displaystyle\frac{7}{4}$.
Answer: Option b: $\displaystyle\frac{7}{4}$.
Key concepts used: Key pattern identification of simplified value of second factor as 1 -- Evaluating trigonometric function values from given value -- Trigonometric basic function derivation principle -- Solving in mind.
The values being simple, the solution can be reached mentally.
Q3. What is the value of $\displaystyle\frac{\sin \theta}{1-\text{cot }\theta}-\displaystyle\frac{\cos \theta}{1-\tan \theta}$?
- $\displaystyle\frac{1}{(\sin \theta-\cos \theta)}$
- $\displaystyle\frac{1}{(\sin \theta+\cos \theta)}$
- $\sin \theta+\cos \theta$
- $\sin \theta-\cos \theta$
Solution 3: Immediate solution by identifying the key pattern that converting both $\tan \theta$ and $\text{cot }\theta$ to $\sin \theta$ and $\cos \theta$ will equalize the denominators and simplify the numerator to 1
Converting both $\tan \theta$ and $\text{cot }\theta$ to $\sin \theta$ and $\cos \theta$, the target expression becomes,
$E=\displaystyle\frac{\sin \theta}{1-\text{cot }\theta}-\displaystyle\frac{\cos \theta}{1-\tan \theta}$
$=\displaystyle\frac{\sin^2 \theta}{\sin \theta-\cos \theta}-\left[\displaystyle\frac{\cos^2 \theta}{\cos \theta-\sin \theta}\right]$
$=\displaystyle\frac{\sin^2 \theta+\cos^2 \theta}{\sin \theta-\cos \theta}=\frac{1}{\sin \theta-\cos \theta}$.
Answer: Option a: $\displaystyle\frac{1}{\sin \theta-\cos \theta}$.
Key concepts used: Key pattern identification of final simplified result by converting both $\tan \theta$ and $\text{cot }\theta$ to $\sin \theta$ and $\cos \theta$ -- Denominator equalization -- Solving in mind.
Q4. The value of $\sin^2 30^0.\cos^2 45^0+2\tan^2 30^0-\text{sec}^2 60^0$ is equal to,
- $-\displaystyle\frac{13}{12}$
- $-\displaystyle\frac{1}{12}$
- $-\displaystyle\frac{77}{24}$
- $-\displaystyle\frac{25}{12}$
Solution 4: Quick solution by directly substituting the trigonometric function values for specific angles
The values of these commonly used trigonometric functions are,
$\sin 30^0=\displaystyle\frac{1}{2}$.
$\cos 45^0=\displaystyle\frac{1}{\sqrt{2}}$.
$\tan 30^0=\displaystyle\frac{1}{\sqrt{3}}$.
$\text{sec }60^0=2$.
Substituting in target expression,
$E=\displaystyle\frac{1}{4}.\displaystyle\frac{1}{2}+\displaystyle\frac{2}{3}-4$
$=\displaystyle\frac{19}{24}-4=-\displaystyle\frac{77}{24}$.
Answer: Option c: $-\displaystyle\frac{77}{24}$.
Key concepts used: Trigonometric function values for specific angles -- Solving in mind.
Q5. If $\tan x=\text{cot }(45^0+2x)$, then what is the value of $x$?
- $20^0$
- $45^0$
- $\displaystyle\frac{45^0}{2}$
- $15^0$
Solution 5: Solve quickly by Complementary angle trigonometric relations
By complementary angle trigonometric relation,
$\tan x=\text{cot }(45^0+2x)=\tan (90^0-45^2-2x)$.
So,
$x=45^0-2x$,
Or, $x=15^0$.
Answer: Option d: $15^0$.
Key concepts used: Trigonometric complementary angle relations -- Solving in mind.
Q6. If $\sin (A+B)=\displaystyle\frac{\sqrt{3}}{2}$ and $\tan (A-B)=\displaystyle\frac{1}{\sqrt{3}}$, then $(2A+3B)$ is equal to,
- $125^0$
- $135^0$
- $120^0$
- $130^0$
Solution 6: Solving in mind by values of trigonometric functions at specific angles and simple algebra
We know, for $\theta=60^0$, $\sin \theta=\displaystyle\frac{\sqrt{3}}{2}$. So from the first equation,
$\sin (A+B)=\displaystyle\frac{\sqrt{3}}{2}=\sin 60^0$,
Or, $(A+B)=60^0$.
Similarly from the second equation,
$\tan (A-B)=\displaystyle\frac{1}{\sqrt{3}}=\tan 30^0$,
Or, $(A-B)=30^0$.
Add the two resulting equations to get the value of $A$,
$2A=90^0$, Or, $A=45^0$.
Subtract the second resulting equation from the first to get value of $B$,
$2B=30^0$, Or, $B=15^0$.
Target expression,
$(2A+3B)=90^0+45^0=135^0$.
Answer: Option b: $135^0$.
Key concepts used: Trigonometric function values at specific angles -- Simple algebraic solution of two linear equations in two variables -- Solving in mind.
Q7. What is the value of $\displaystyle\frac{\text{cot }x}{1-\tan x}+\displaystyle\frac{\tan x}{1-\text{cot }x}$?
- $\text{sec}^2 x.\text{cosec}^2 x+1$
- $\tan x.\text{cot }x+1$
- $\sin x\cos x+1$
- $\text{sec } x.\text{cosec } x+1$
Solution 7: Quick solution by equalizing denominators to $(1-\tan x)$
Denominator equalization of the two fraction terms to $(1-\tan x)$ by replacing $\text{cot }x$ by $\tan x$ in second denominator should give us the quickest answer,
$E=\displaystyle\frac{\text{cot }x}{1-\tan x}+\displaystyle\frac{\tan x}{1-\text{cot }x}$
$=\displaystyle\frac{\text{cot }x}{1-\tan x}-\displaystyle\frac{\tan^2 x}{1-\tan x}$
$=\displaystyle\frac{\text{cot }x-\tan^2 x}{1-\tan x}$.
Now identify the key pattern that when you convert the $\text{cot }x$ to $\tan x$, you will get $1-\tan^3 x$ in the numerator and as a result, the factor $(1-\tan x)$ will get cancelled out,
$E=\displaystyle\frac{1-\tan^3 x}{\tan x(1-\tan x)}$,
$=\displaystyle\frac{(1-\tan x)(1+\tan x+\tan^2 x)}{\tan x(1-\tan x)}$,
$=\displaystyle\frac{\text{sec}^2 x+\tan x}{\tan x}$, replacing $1+\tan^2 x$ by $\text{sec}^2 x$,
$=\text{sec } x.\text{cosec } x+1$.
Answer: Option d: $\text{sec } x.\text{cosec } x+1$.
Key concepts used: Denominator equalization that always produces positive and quick results -- Key pattern identification of $(1-\tan x)$ in denominator getting cancelled out by two factor expansion of $(1-\tan^3 x)$ in the numerator -- Sum of cubes factorization -- Solving in mind.
Q8. What is the least value of $15\cos^2 \theta+17\sin^2 \theta$?
- $2$
- $18$
- $15$
- $14$
Solution 8: Immediate solution by basic trigonometric relation of $\sin^2 \theta +\cos^2 \theta=1$ and minimum value of $\sin^2 \theta$ as 0 concept
It is easy to simplify the given expression,
$15\cos^2 \theta+17\sin^2 \theta$
$=15(\sin^2 \theta+\cos^2 \theta)+2\sin^2 \theta$
$=15+2\sin^2 \theta$.
You need to be a little careful at this point because, value of $\sin \theta$ varies from its minimum $-1$ to $0$ to its maximum $+1$. But when you raise $\sin \theta$ to its square, the minimum $-1$ is squared to $+1$.
So the least value of $\sin^2 \theta$ becomes just $0$, and of the target expression,
$15+0=15$.
Answer: Option c: $15$.
Key concepts used: Basic trigonometry relation of $\sin^2 \theta+\cos^2 \theta=1$ -- Minimum value of $\sin^2 \theta$ -- Least value of square of trigonometric function -- Solving in mind.
Q9. If $\cos 37^0=\displaystyle\frac{a}{b}$ then what is the value of $\text{cosec }37^0-\cos 53^0$?
- $\displaystyle\frac{b\sqrt{a^2+b^2}}{a}$
- $\displaystyle\frac{b^2-a^2}{ab}$
- $\displaystyle\frac{a^2}{b\sqrt{a^2+b^2}}$
- $\displaystyle\frac{a^2}{b\sqrt{b^2-a^2}}$
Solution 9: Solve quickly by converting $\cos 53^0$ to $\sin 37^0$ using complementary angle trigonometric relation and deriving value of $\sin 37^0$ from given value
By trigonometric complementary angle relation,
$\cos \theta=\sin (90^0-\theta)$ where $\theta$ is acute.
So,
$\cos 53^0=\sin(90^0-57^0)=\sin 37^0$.
From given value of $\cos 37^0$ we will now evaluate $\sin 37^0$,
$\sin 37^0=\sqrt{1-\cos^2 37^0}=\displaystyle\frac{1}{b}\sqrt{b^2-a^2}$.
Substitute the results in the target expression
$E=\text{cosec }37^0-\cos 53^0$
$=\displaystyle\frac{1}{\sin 37^0}-\sin 37^0$
$=\displaystyle\frac{1-\sin^2 37^0}{\sin 37^0}$
$=\displaystyle\frac{\cos^2 37^0}{\sin 37^0}$
The target expression is simplified as much as possible before substitution of values of variables. This strategy always produces quicker solution with less calculation. This is what we call, Target expression simplification first strategy.
So,
$E=\displaystyle\frac{\displaystyle\frac{a^2}{b^2}}{\displaystyle\frac{\sqrt{b^2-a^2}}{b}}$
$=\displaystyle\frac{a^2}{b\sqrt{b^2-a^2}}$.
Answer: Option d: $\displaystyle\frac{a^2}{b\sqrt{b^2-a^2}}$.
Key concepts used: Trigonometric complementary angle relation -- Target expression simplification first strategy -- Solving in mind.
Q10. If $\displaystyle\frac{\text{cot}^2 x}{(1+\sqrt{3})}+\displaystyle\frac{1}{2}(3-\sqrt{3})=\text{cot }x$, what is the value of $x$?
- $\displaystyle\frac{\pi}{2}$, $\displaystyle\frac{\pi}{4}$
- $\pi$, $\displaystyle\frac{\pi}{4}$
- $\displaystyle\frac{\pi}{6}$, $\displaystyle\frac{\pi}{4}$
- $\displaystyle\frac{\pi}{6}$, $\displaystyle\frac{\pi}{2}$
Solution 10: Quick solution by strategic formation of a quadratic equation and solving it for two values of $\text{cot }x$
With powers of $\text{cot }x$ in the given equation matching with those of a quadratic equation, as well as from the two values of $x$ in the choices, it is clear that we need to form a quadratic equation in $\text{cot }x$ as easily as possible for a quick solution.
The first step is to multiply the equation all through by the surd factor $(\sqrt{3}+1)$ to,
- convert the coefficient of $\text{cot}^2 x$ to the simplest value of 1
- get rid of the surd denominator at one stroke, and,
- convert the numeric term to a simple $\sqrt{3}$, which is surd simplification.
The result of the action is,
$\displaystyle\frac{\text{cot}^2 x}{(1+\sqrt{3})}+\displaystyle\frac{1}{2}(3-\sqrt{3})=\text{cot }x$,
Or, $\text{cot}^2 x+\displaystyle\frac{1}{2}\sqrt{3}(\sqrt{3}-1)(\sqrt{3}+1)=(\sqrt{3}+1)\text{cot }x$,
Or, $\text{cot}^2 x-(\sqrt{3}+1)\text{cot }x+\sqrt{3}=0$.
This quadratic polynomial on the LHS can easily be factorized to,
$(\text{cot }x-1)(\text{cot }x-\sqrt{3})=0$.
The two roots are,
$\text{cot }x=1$, Or, $x=45^0=\displaystyle\frac{\pi}{4}$, and,
$\text{cot }x=\sqrt{3}$, Or, $x=30^0=\displaystyle\frac{\pi}{6}$.
Answer: Option c: $\displaystyle\frac{\pi}{6}$, $\displaystyle\frac{\pi}{4}$.
Key concepts used: Problem analysis and goal formation -- Surd factoring of $(3-\sqrt{3})$ to $\sqrt{3}(\sqrt{3}-1)$ -- Surd simplification -- Quadratic equation solving by factorization -- Solving in mind.
Yes, the problem can easily be solved in mind if you are comfortable with surds and quadratic equations. In this case the equation is very suitable for ready factorization and finding the roots.
End note
Observe that, each of the problems could be quickly and cleanly solved in minimum number of steps using special key patterns and methods in each case.
This is the hallmark of quick problem solving:
- Concept based pattern and method formation, and,
- Identification of the key pattern and use of the method associated with it. Every special pattern has its own method, and not many such patterns are there.
Important is the concept based pattern identification and use of quick problem solving method.
SSC CPO level Question and Solution sets
Algebra
SSC CPO level Solved Question set 1 on Algebra 1
SSC CPO level Solved Question set 2 on Algebra 2
Trigonometry
SSC CPO level Solved Question set 3 on Trigonometry 1
SSC CPO level Solved Question set 4 on Trigonometry 2
Number system
SSC CPO level Solved Question set 5 on Number system 1
Surds and Indices
SSC CPO level Solved Question set 6 on Surds and indices 1
