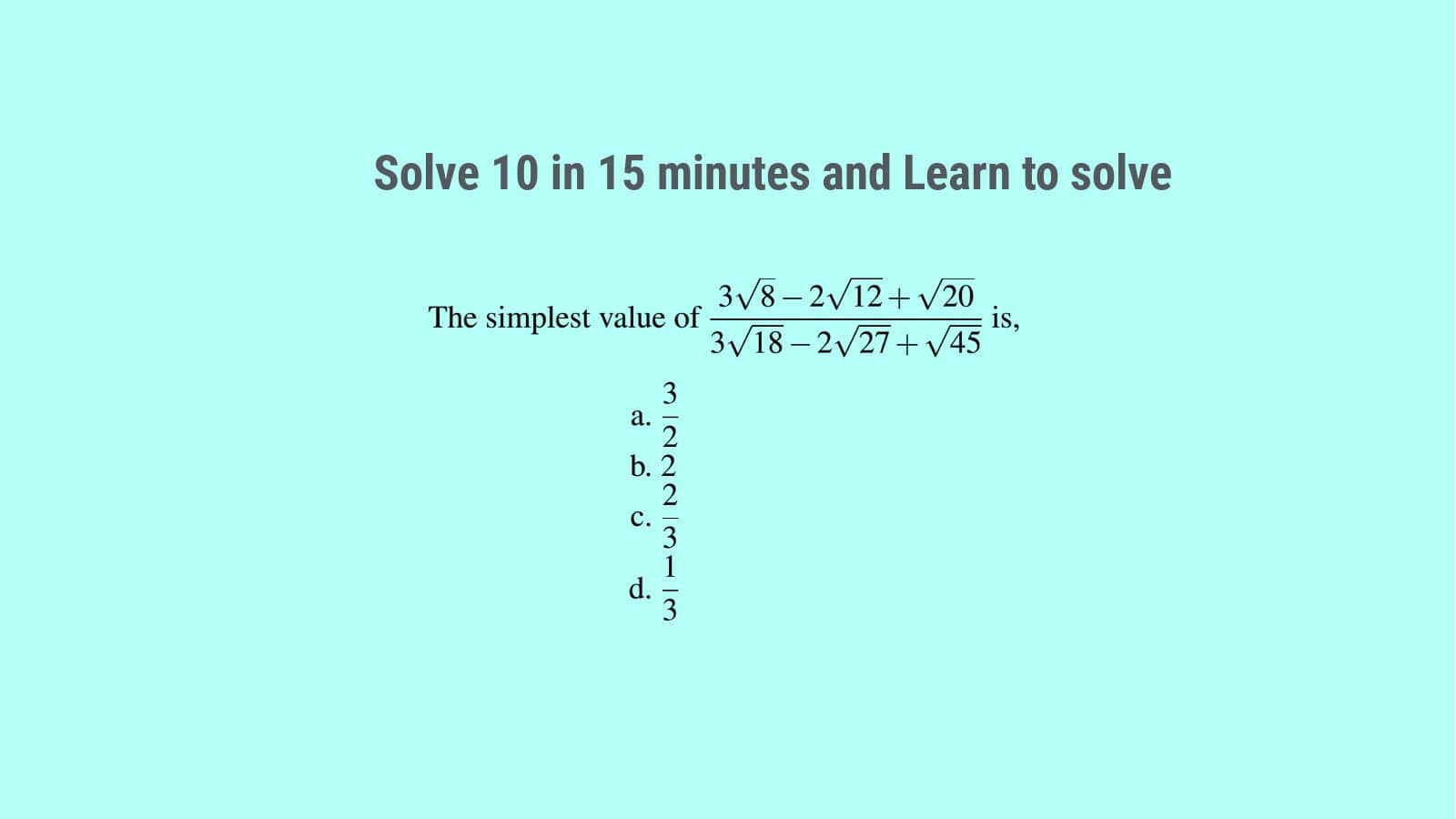
Surds and indices questions solved set 91 for SSC CGL
Solve 10 surds and indices questions for SSC CGL set 91 in 15 minutes. Verify correctness from answers and finally learn how to solve from solutions.
The solved question set contains,
- Surds and indices questions for SSC CGL to be answered in 15 minutes (10 chosen questions)
- Answers to the questions, and,
- Detailed conceptual solutions to the questions.
For maximum gains, the test should be taken first, and then the solutions are to be read.
The answers and detailed solutions follow the questions.
First try to solve the questions yourself and then go through the solutions.
All problems are solved by specially quick methods based on discovered patterns.
10 surds and indices questions SSC CGL Set 91 - answering time 15 mins
Q1. If $\sqrt{5x-6}+\sqrt{5x+6}=6$, then what is the value $x$?
- $0$
- $-4$
- $4$
- $2$
Q2. The ascending order of $(2.89)^{0.5}$, $2-(0.5)^2$, $\sqrt{3}$, and $\sqrt[3]{0.0008}$ is,
- $2-(0.5)^2$, $\sqrt{3}$, $\sqrt[3]{0.0008}$, $(2.89)^{0.5}$
- $\sqrt{3}$, $\sqrt[3]{0.0008}$, $2-(0.5)^2$, $(2.89)^{0.5}$
- $\sqrt[3]{0.0008}$, $(2.89)^{0.5}$, $\sqrt{3}$, $2-(0.5)^2$
- $\sqrt[3]{0.0008}$, $\sqrt{3}$, $(2.89)^{0.5}$, $2-(0.5)^2$
Q3. The value of $\displaystyle\frac{2+\sqrt{3}}{2-\sqrt{3}}+\displaystyle\frac{2-\sqrt{3}}{2+\sqrt{3}}+\displaystyle\frac{\sqrt{3}+1}{\sqrt{3}-1}$ is,
- $16 +\sqrt{3}$
- $4-\sqrt{3}$
- $2-\sqrt{3}$
- $2+\sqrt{3}$
Q4. Simplify $\left[\displaystyle\frac{\displaystyle\frac{3}{2+\sqrt{3}}-\displaystyle\frac{2}{2-\sqrt{3}}}{2-\sqrt{5}}\right]$.
- $\displaystyle\frac{1}{2}-5\sqrt{3}$
- $2-5\sqrt{3}$
- $0$
- $1$
Q5. The simplest value of $\displaystyle\frac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}$ is,
- $\displaystyle\frac{3}{2}$
- $2$
- $\displaystyle\frac{2}{3}$
- $\displaystyle\frac{1}{3}$
Q6. $(2^{51}+2^{52}+2^{53}+2^{54}+2^{55})$ is divisible by,
- $124$
- $23$
- $127$
- $58$
Q7. If $x+\sqrt{5}=5+\sqrt{y}$ and $x$, $y$ are positive integers, then the value of $\displaystyle\frac{\sqrt{x}+y}{x+\sqrt{y}}$ is,
- $\sqrt{5}$
- $1$
- $2$
- $5$
Q8. If $p=9$, $q=\sqrt{17}$ then the value of $(p^2-q^2)^{-\frac{1}{3}}$
- $4$
- $3$
- $\displaystyle\frac{1}{4}$
- $\displaystyle\frac{1}{3}$
Q9. If $x=2+\sqrt{3}$, then the value of $\displaystyle\frac{x^2-x+1}{x^2+x+1}$ is,
- $\displaystyle\frac{2}{3}$
- $\displaystyle\frac{3}{4}$
- $\displaystyle\frac{3}{5}$
- $\displaystyle\frac{4}{5}$
Q10. If $\displaystyle\frac{1}{\sqrt{a}}-\displaystyle\frac{1}{\sqrt{b}}=0$, then the value of $\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}$
- $\displaystyle\frac{1}{\sqrt{ab}}$
- $\displaystyle\frac{1}{2\sqrt{ab}}$
- $\sqrt{ab}$
- $\displaystyle\frac{2}{\sqrt{ab}}$
Answers to the surds and indices questions SSC CGL set 91
Q1. Answer: Option d: $2$.
Q2. Answer: Option c: $\sqrt[3]{0.0008}$, $(2.89)^{0.5}$, $\sqrt{3}$, $2-(0.5)^2$.
Q3. Answer: Option a: $16 +\sqrt{3}$.
Q4. Answer: Option d: $1$.
Q5. Answer: Option c: $\displaystyle\frac{2}{3}$.
Q6. Answer: Option a: $124$.
Q7. Answer: Option b: $1$.
Q8. Answer: Option c: $\displaystyle\frac{1}{4}$.
Q9. Answer: Option c: $\displaystyle\frac{3}{5}$.
Q10. Answer: Option d: $\displaystyle\frac{2}{\sqrt{ab}}$.
Solution to the surds and indices questions SSC CGL Set 91 - answering time was 15 mins
Q1. If $\sqrt{5x-6}+\sqrt{5x+6}=6$, then what is the value $x$?
- $0$
- $-4$
- $4$
- $2$
Solution 1: Instant intuitive solution by trying out choice values
You would be able to get the answer practically instantly with or without trying out the choice values.
If you try $x=2$ at option d, the equation is satisfied.
Answer: Option d: $2$.
Key concepts used: Choice value test -- Intuitive solution -- Solving in mind.
Note: Though you got your answer by trial, don't think deductive solution is too hard.
Given equation,
$\sqrt{5x-6}+\sqrt{5x+6}=6$.
Raise it to its square,
$(5x-6)+2\sqrt{25x^2-36}+(5x+6)=36$,
Or, $5x-18=-\sqrt{25x^2-36}$, common factor 2 cancelled out.
Raise to square again,
$25x^2-180x+18^2=25x^2-36$,
Or, $180x=18^2+2\times{18}=20\times{18}$,
Or, $x=2$.
Q2. The ascending order of $(2.89)^{0.5}$, $2-(0.5)^2$, $\sqrt{3}$, and $\sqrt[3]{0.0008}$ is,
- $2-(0.5)^2$, $\sqrt{3}$, $\sqrt[3]{0.0008}$, $(2.89)^{0.5}$
- $\sqrt{3}$, $\sqrt[3]{0.0008}$, $2-(0.5)^2$, $(2.89)^{0.5}$
- $\sqrt[3]{0.0008}$, $(2.89)^{0.5}$, $\sqrt{3}$, $2-(0.5)^2$
- $\sqrt[3]{0.0008}$, $\sqrt{3}$, $(2.89)^{0.5}$, $2-(0.5)^2$
Solution 2: Quick solution by conversion to simple decimals and problem breakdown technique
At first step, leaving $\sqrt{3}$, convert rest three of the four given numbers to simple decimals of unit power. This is applying problem breakdown technique.
Again, for ease of comparison when powers of the three numbers are converted to 1, essentially base equalization technique is used.
So convert to three easy decimals of unit power for ranking these three first,
$(2.89)^{0.5}=\sqrt{2.89}=1.7$,
$2-(0.5)^2=2-0.25=1.75$, and,
$\sqrt[3]{0.0008}=0.2$.
Calculating decimal equivalent of $\sqrt{3}$ is avoided, but we are sure that $1.7 \lt \sqrt{3}$ as,
$(1.7)^2=2.89 \lt 3$.
Rank the three decimal values obtained in ascending order,
$0.2 \lt 1.7 \lt 1.75$,
Or, $\sqrt[3]{0.0008} \lt (2.89)^{0.5} \lt 2-(0.5)^2$.
Test now whether $(1.75)^2$ is greater or lesser than 3 to make the final ranking order.
A quick hand calculation reveals,
$(1.75)^2 > 3$,
Or, $\sqrt{3} \lt 1.75$.
Final ascending order ranking is then,
$0.2 \lt 1.7 \lt \sqrt{3} \lt 1.75$,
Or, $\sqrt[3]{0.0008} \lt (2.89)^{0.5} \lt \sqrt{3} \lt 2-(0.5)^2$.
Answer: Option c: $\sqrt[3]{0.0008}$, $(2.89)^{0.5}$, $\sqrt{3}$, $2-(0.5)^2$.
Key concepts used: Cube root of a decimal -- Square root of a decimal -- Problem breakdown technique -- Number ranking by comparison -- Base equalization technique.
Q3. The value of $\displaystyle\frac{2+\sqrt{3}}{2-\sqrt{3}}+\displaystyle\frac{2-\sqrt{3}}{2+\sqrt{3}}+\displaystyle\frac{\sqrt{3}+1}{\sqrt{3}-1}$ is,
- $16 +\sqrt{3}$
- $4-\sqrt{3}$
- $2-\sqrt{3}$
- $2+\sqrt{3}$
Solution 3: Quick solution by surd rationalization and simplification
Rationalize the denominators of the three terms by multiplying both numerator and denominator of the terms respectively by $(2+\sqrt{3})$, $(2-\sqrt{3})$, and $(\sqrt{3}+1)$. First two denominators turn to 1 and the third to 2. Result is,
$(2+\sqrt{3})^2+(2-\sqrt{3})^2+\displaystyle\frac{(\sqrt{3}+1)^2}{2}$
$=7\times{2}+2+\sqrt{3}=16+\sqrt{3}$.
Answer: Option a: $16 +\sqrt{3}$.
Key concepts used: Surd rationalization -- Surd simplification -- Solving in mind.
Q4. Simplify $\left[\displaystyle\frac{\displaystyle\frac{3}{2+\sqrt{3}}-\displaystyle\frac{2}{2-\sqrt{3}}}{2-\sqrt{5}}\right]$.
- $\displaystyle\frac{1}{2}-5\sqrt{3}$
- $2-5\sqrt{3}$
- $0$
- $1$
Solution 4: Quick solution by simplifying the numerator terms by direct cross-multiplication
Directly cross-multiply the numerators and denominators of the two terms of the main numerator,
$\left[\displaystyle\frac{\displaystyle\frac{3}{2+\sqrt{3}}-\displaystyle\frac{2}{2-\sqrt{3}}}{2-\sqrt{5}}\right]$
$=\displaystyle\frac{3(2-\sqrt{3})-2(2+\sqrt{3})}{2-\sqrt{5}}$, as $(2+\sqrt{3})(2+\sqrt{3})=4-3=1$
$=\displaystyle\frac{2-5\sqrt{3}}{2-5\sqrt{3}}$
$=1$.
Answer: Option d: $1$.
Key concepts used: Surd simplification -- Solving in mind.
Q5. The simplest value of $\displaystyle\frac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}$ is,
- $\displaystyle\frac{3}{2}$
- $2$
- $\displaystyle\frac{2}{3}$
- $\displaystyle\frac{1}{3}$
Solution 5: Quick solution by surd term factoring and key pattern identification
Factor out the squares embedded in the square roots of the numerator and denominator terms,
$E=\displaystyle\frac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}$
$=\displaystyle\frac{6\sqrt{2}-4\sqrt{3}+2\sqrt{5}}{9\sqrt{2}-6\sqrt{3}+3\sqrt{5}}$.
Identify the key pattern that if you factor out 2 from numerator terms and 3 from denominator terms, the numerator and denominator cancel out,
$E=\displaystyle\frac{2(3\sqrt{2}-2\sqrt{3}+\sqrt{5})}{3(3\sqrt{2}-2\sqrt{3}+\sqrt{5})}$
$=\displaystyle\frac{2}{3}$.
Answer: Option c: $\displaystyle\frac{2}{3}$.
Key concepts used: Surd term factoring -- Key pattern identification -- Solving in mind.
Q6. $(2^{51}+2^{52}+2^{53}+2^{54}+2^{55})$ is divisible by,
- $124$
- $23$
- $127$
- $58$
Solution 6: Quick solution by common term factoring and choice value matching
This is a problem on indices.
Take out the common factor $2^{51}$ from the four terms,
$(2^{51}+2^{52}+2^{53}+2^{54}+2^{55})$
$=2^{51}(1+2+4+8+16)$
$=2^{51}\times{31}$
$=2^{49}\times{124}$.
$2^2=4$ is taken out from $2^{51}$ and multiplied with the second factor $31$ so that you get $124$ that matches with the choice value 'a'.
So, $124$ is the desired factor of the given target expression.
Answer: Option a: $124$.
Key concepts used: Factoring out common factor -- Key pattern identification -- Choice value matching-- Solving in mind.
Note: Choice value matching is a little different from Choice value test. When the answer is obtained with certainty without looking at the choice values and then its form is changed to match one of the choice values, we are using Choice value matching technique.
On the other hand, in Choice value test, the answer itself is obtained by testing each choice value against a given information. This is the more frequently used technique for solving MCQs.
Q7. If $x+\sqrt{5}=5+\sqrt{y}$ and $x$, $y$ are positive integers, then the value of $\displaystyle\frac{\sqrt{x}+y}{x+\sqrt{y}}$ is,
- $\sqrt{5}$
- $1$
- $2$
- $5$
Solution 7: Quick solution by Surd term comparison between RHS and LHS
In the given equation $x+\sqrt{5}=5+\sqrt{y}$, the surd terms in the LHS and RHS respectively are, $\sqrt{5}$ and $\sqrt{y}$.
By surd property, an irrational surd cannot be added to a rational integer. As $x$ and $y$ both are integers, the only surd $\sqrt{5}$ on LHS must have an equal surd on RHS.
The only possible surd candidate being $\sqrt{y}$ on the RHS then,
$\sqrt{5}=\sqrt{y}$,
Or, $y=5$.
Substituting,
$x=5$.
The target equation,
$\displaystyle\frac{\sqrt{x}+y}{x+\sqrt{y}}=\frac{5+\sqrt{5}}{5+\sqrt{5}}=1$.
Answer: Option b: $1$.
Key concepts used: Surd term comparison -- Basic surd property -- Solving in mind.
Q8. If $p=9$, $q=\sqrt{17}$ then the value of $(p^2-q^2)^{-\frac{1}{3}}$
- $4$
- $3$
- $\displaystyle\frac{1}{4}$
- $\displaystyle\frac{1}{3}$
Solution 8: Quick solution by direct simplification using indices concepts
Substitute given values of $p$ and $q$ in the target expression,
$(p^2-q^2)^{-\frac{1}{3}}$
$=(81-17)^{-\frac{1}{3}}$
$=\displaystyle\frac{1}{(64)^{\frac{1}{3}}}=\frac{1}{\sqrt[3]{64}}=\frac{1}{4}$.
Answer: Option c: $\displaystyle\frac{1}{4}$.
Key concepts used: Indices concepts -- Solving in mind.
Q9. If $x=2+\sqrt{3}$, then the value of $\displaystyle\frac{x^2-x+1}{x^2+x+1}$ is,
- $\displaystyle\frac{2}{3}$
- $\displaystyle\frac{3}{4}$
- $\displaystyle\frac{3}{5}$
- $\displaystyle\frac{4}{5}$
Solution 9: Quick solution by key pattern identification of Componendo dividendo on target expression and surd rationalization
This is a special problem that needs special treatment.
Identify the key pattern that the target expression conforms perfectly to the powerful method of Componendo dividendo as it displays the signature of Componendo dividendo in the form of,
$\displaystyle\frac{a-b}{a+b}$, where $a=x^2+1$ and $b=x$.
Observe that both pairs of terms in numerator and denominator, $a$ and $b$ are same except that one pair of terms of same value $b$ are of opposite sign.
This is what we call, the signature pattern of Componendo dividendo and is the ideal condition for applying the three-step Componendo dividendo method mentally and arrive at a very much simplified result quickly.
To apply this method on the target expression that has no value assigned, assume a dummy value $p$ for the target expression,
$\displaystyle\frac{x^2-x+1}{x^2+x+1}=\frac{a-b}{a+b}=p$.
In the first step of componendo dividendo, add 1 to both sides,
$\displaystyle\frac{2a}{a+b}=p+1$.
In the second step, subtract both sides from 1,
$\displaystyle\frac{2b}{a+b}=1-p$.
In the third step, divide the first result by the second to eliminate the common denominator of the LHS,
$\displaystyle\frac{a}{b}=\frac{p+1}{1-p}$,
Or, $\displaystyle\frac{x^2+1}{x}=x+\displaystyle\frac{1}{x}=\displaystyle\frac{p+1}{1-p}$.
Now only, substitute the given value of $x=2+\sqrt{3}$,
$\displaystyle\frac{p+1}{1-p}=(2+\sqrt{3})+\displaystyle\frac{1}{2+\sqrt{3}}$.
Rationalizing the denominator of the second term by multiplying both numerator and denominator by $(2-\sqrt{3})$,
$\displaystyle\frac{p+1}{1-p}=(2+\sqrt{3})+(2-\sqrt{3})=4$.
Cross-multiply,
$p+1=4-4p$,
Or, $\text{Target expression}=p=\displaystyle\frac{3}{5}$.
Though showing the steps in details took time and space, being simple and conceptual, these can easily be carried out in mind.
Answer: Option c: $\displaystyle\frac{3}{5}$.
Key concepts used: Key pattern identification -- Signature pattern of componendo dividendo -- Componendo dividendo on target expression using dummy variable -- Surd rationalization -- Surd algebra.
Q10. If $\displaystyle\frac{1}{\sqrt{a}}-\displaystyle\frac{1}{\sqrt{b}}=0$, then the value of $\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}$
- $\displaystyle\frac{1}{\sqrt{ab}}$
- $\displaystyle\frac{1}{2\sqrt{ab}}$
- $\sqrt{ab}$
- $\displaystyle\frac{2}{\sqrt{ab}}$
Solution 10: Quick solution by identifying $a=b$ from given equation and choice value matching
Given equation,
$\displaystyle\frac{1}{\sqrt{a}}-\displaystyle\frac{1}{\sqrt{b}}=0$,
Or, $\displaystyle\frac{1}{\sqrt{a}}=\displaystyle\frac{1}{\sqrt{b}}$,
Or, $a=b$.
Substitute $a=b$ in target expression,
$\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}$
$=\displaystyle\frac{2}{a}$.
Match the choice value of option d with this target expression value,
$\displaystyle\frac{2}{\sqrt{ab}}=\frac{2}{\sqrt{a^2}}=\frac{2}{a}$.
Answer: Option d: $\displaystyle\frac{2}{\sqrt{ab}}$.
Key concepts used: Choice value matching with simplified target expression value -- Solving in mind.
End note
Observe that, each of the problems could be quickly and cleanly solved in minimum number of steps using special key patterns and methods in each case.
This is the hallmark of quick problem solving:
- Concept based pattern and method formation, and,
- Identification of the key pattern and use of the method associated with it. Every special pattern has its own method, and not many such patterns are there.
Important is the concept based pattern identification and use of quick problem solving method.
Guided help on Fractions, Surds and Indices in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on fractions, surds and indices in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Fractions, Surds and Indices and relevant topics in Suresolv and is up-to-date.
